Câu hỏi:
2 năm trước
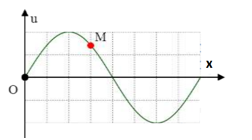
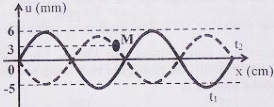
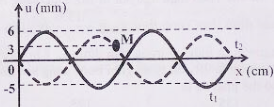
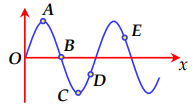
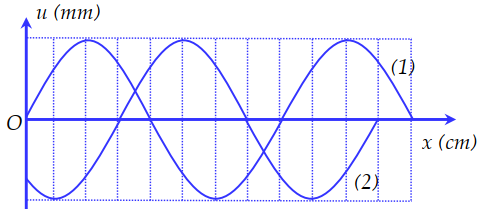
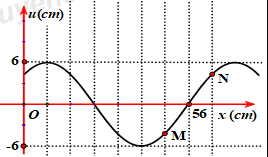
Một nguồn phát sóng cơ hình sin đặt tại O, truyền dọc theo sợi dây đàn hồi căng ngang rất dài OA với bước sóng \(24cm\). Tại thời điểm \({t_1}\) và \({t_2}\) hình dạng của một đoạn dây tương ứng như đường 1 và đường 2 của hình vẽ, trục Ox trùng với vị trí cân bằng của sợi dây, chiều dương trùng với chiều truyền sóng. Trong đó, M là điểm cao nhất, \({u_M},{\rm{ }}{u_N},{\rm{ }}{u_H}\) lần lượt là li độ của các điểm M, N, H. Biết \(u_M^2 = u_{N}^2 + u_H^2\) và biên độ sóng không đổi. Khoảng cách từ P đến Q bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
- Tại thời điểm \({t_1}\), điểm H có li độ \({u_H}\) và đang tăng lên.
Đến thời điểm \({t_2}\), điểm H có li độ vẫn là \({u_H}\) và đang giảm
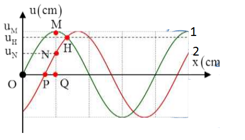
- Biểu diễn trên vòng tròn lượng giác, ta được:
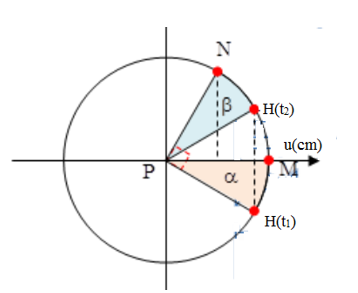
Ta có: \(u_M^2 = u_{N}^2 + u_H^2 \to \angle NP{H_{{t_1}}} = {90^0}\)
Ta để ý rằng vị trí từ \(M\) đến \({H_{{t_1}}}\) ứng với sự lệch pha nhau về mặt không gian \(\left( {\Delta x} \right)\), vị trí từ \(N\) đến \({H_{{t_1}}}\) ứng với sự lệch pha về mặt thời gian \(\left( {\Delta t} \right)\)
Mặt khác \(M\) và \(N\) có cùng một vị trí trong không gian và \({u_{{H_{{t_1}}}}} = {u_{{H_{{t_2}}}}} \to \alpha = \beta = {30^0}\)
Từ đó, ta có:
\(\begin{array}{l}{u_N} = \frac{A}{2} \to \Delta {\varphi _{{x_{PQ}}}} = \frac{{2\pi PQ}}{\lambda } = \frac{\pi }{6}\\ \to PQ = \frac{\lambda }{{12}} = \frac{{24}}{{12}} = 2cm\end{array}\)
Hướng dẫn giải:
+ Đọc đồ thị và áp dụng các công thức sóng cơ học.
+ Sử dụng vòng tròn lượng giác
+ Áp dụng công thức tính độ lệch pha: \(\Delta \varphi = \frac{{2\pi \Delta x}}{\lambda }\)
Câu hỏi khác
- Bài tập các đại lượng đặc trưng của sóng cơ học có đáp án MÔN LÝ lớp 12
- Bài tập lí thuyết về sóng cơ và sự truyền sóng cơ có đáp án MÔN LÝ lớp 12
- Bài tập lý thuyết chung về giao thoa sóng có lời giải MÔN LÝ lớp 12
- Bài tập đồ thị sóng cơ học có đáp án MÔN LÝ lớp 12
- Bài tập phương trình sóng cơ học có đáp án MÔN LÝ lớp 12
