Một khung dây dẫn có 100 vòng. Diện tích giới hạn bởi mỗi vòng dây là \(S = 50c{m^2}\). Đặt khung dây trong từ trường đều \(B = 0,2T\) với các đường cảm ứng từ hợp với mặt phẳng khung một góc \(\alpha = {30^0}\). Từ thông qua khung có độ lớn là:
Trả lời bởi giáo viên
Theo bài ra ta có :
\(\left\{ \begin{array}{l}S = 500\left( {c{m^2}} \right) = {50.10^{ - 4}}\left( {{m^2}} \right) = {5.10^{ - 3}}\left( {{m^2}} \right)\\N = 100\\B = 0,2T\\\alpha = \left( {\overrightarrow n ,\overrightarrow B } \right) = {90^0} - {30^0} = {60^0}\end{array} \right.\)
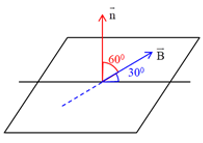
Từ thông qua khung có độ lớn là:
\(\Phi = N.B.S.cos\alpha = 100.0,{2.5.10^{ - 3}}.cos60 = 0,05Wb\)
Hướng dẫn giải:
Công thức tính từ thông: \(\Phi = N.B.S.cos\alpha \)
Trong đó:
+ N là số vòng dây.
+ B là cảm ứng từ \(\left( T \right)\)
+ S là diện tích mạch kín \(\left( {{m^2}} \right)\)
+ \(\alpha = \left( {\overrightarrow B ,\overrightarrow n } \right)\) , \(\overrightarrow n \) là véc tơ pháp tuyến của mặt phẳng chứa mạch kín.
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 3 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
