Cho hình chóp đều $S . A B C D$ có cạnh $2a$, cạnh bên \(a\sqrt 3 \). Góc giữa mặt bên và mặt đáy bằng:
Trả lời bởi giáo viên
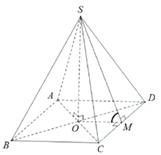
Ta có: góc giữa mặt bên và mặt đáy là góc giữa \((SCD)\) và \((ABCD)\).
Gọi \(O = AC \cap BD\). Vì $S . A B C D$ là hình chóp đều nên \(SO \bot (ABCD)\).
Gọi \(M\) là trung điểm $C D$. Ta có: \(\left\{ {\begin{array}{*{20}{l}}{CD \bot SM}\\{CD \bot OM}\end{array} \Rightarrow CD \bot (SOM)} \right.\).
Xét hình vuông $A B C D$ ta có: \(OM = a\) và \(OD = \dfrac{{BD}}{2} = \dfrac{{AB\sqrt 2 }}{2} = \dfrac{{2a\sqrt 2 }}{2} = a\sqrt 2 \).
Xét tam giác SOD vuông tại \(O\), ta có: \(SO = \sqrt {S{D^2} - O{D^2}} = \sqrt {{{(a\sqrt 3 )}^2} - {{(a\sqrt 2 )}^2}} = a\).
Xét tam giác SMO vuông tại \(O\), ta có: \(\tan \widehat {SMO} = \dfrac{{SO}}{{OM}} = \dfrac{a}{a} = 1 \Rightarrow \widehat {SMO} = {45^\circ }\).
Hướng dẫn giải:
Ta có: Góc giữa mặt bên và mặt đáy là góc giữa \((SCD)\) và \((ABCD)\).
Gọi \(O = AC \cap BD\). Vì $S . A B C D$ là hình chóp đều nên \(SO \bot (ABCD)\).
=> Từ đó xác định góc giữa mặt bên và mặt đáy.
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
