Cho hình lăng trụ $A B C \cdot A^{\prime} B^{\prime} C^{\prime}$ có đáy $A B C$ là tam giác đều tâm $O$, cạnh $a$, hình chiếu của $C^{\prime}$ trên $\operatorname{mp}(A B C)$ trìng vói tâm của đáy. Cạnh bên CC’ hợp với $m p(A B C)$ góc $60^{\circ}$. Gọi $\mathrm{I}$ là trung điểm của $\mathrm{AB}$. Tính các khoảng cách từ điểm $\mathrm{O}$ đến đường thẳng $\mathrm{CC}^{\prime}$

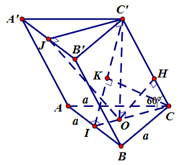
Theo giả thiết, suy ra: \({{\rm{C}}^\prime }{\rm{O}} \bot ({\rm{ABC}})\), suy ra:

\(\left( {\widehat {{\rm{C}}{{\rm{C}}^\prime },({\rm{ABC}})}} \right) = \widehat {{{\rm{C}}^\prime }{\rm{CO}}}\)

Theo giả thiết, ta có: \(\widehat {{{\rm{C}}^\prime }{\rm{CO}}} = {60^\circ }\)

Trong \({\mathop{\rm mp}\nolimits} \left( {{{\rm{C}}^\prime }{\rm{CO}}} \right)\) dựng \({\rm{OH}} \bot {\rm{C}}{{\rm{C}}^\prime }\) tại \({\rm{H}}\) ta được: \({\rm{d}}\left( {{\rm{O}},{\rm{C}}{{\rm{C}}^\prime }} \right) = {\rm{OH}}\).

Xét \(\Delta {\rm{COH}} \Rightarrow {\rm{OH}} = {\rm{OC}} \cdot \sin {30^\circ } = \dfrac{2}{3} \cdot \dfrac{{{\rm{a}}\sqrt 3 }}{2} \cdot \dfrac{{\sqrt 3 }}{2} = \dfrac{{\rm{a}}}{2}\)

Suy ra: \({\rm{d}}\left( {{\rm{O}},{\rm{C}}{{\rm{C}}^\prime }} \right) = \dfrac{{\rm{a}}}{2}\).