Điền số nguyên hoặc phân số dạng a/b vào chỗ trống
Gọi \(G\) là trọng tâm tứ diện \({\rm{ABCD}}\). Gọi \({{\rm{A}}^\prime }\) là trọng tâm của tam giác \({\rm{BCD}}\). Tỉ số \(\dfrac{{GA}}{{G{A^\prime }}}\) bằng:
Trả lời bởi giáo viên
Gọi \(G\) là trọng tâm tứ diện \({\rm{ABCD}}\). Gọi \({{\rm{A}}^\prime }\) là trọng tâm của tam giác \({\rm{BCD}}\). Tỉ số \(\dfrac{{GA}}{{G{A^\prime }}}\) bằng:
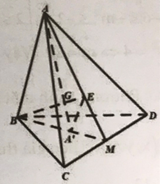
Gọi \(E\) là trọng tâm của tam giác $A C D$, \(M\) là trung điểm của $C D$. Nối \({\rm{BE}}\) cắt \({\rm{A}}{{\rm{A}}^\prime }\) tại \({\rm{G}}\) suy ra \({\rm{G}}\) là trọng tâm tứ diện.
Xét tam giác $M A B$, có \(\dfrac{{ME}}{{MA}} = \dfrac{{M{A^\prime }}}{{MB}} = \dfrac{1}{3}\) suy ra \({A^\prime }E//AB\).
\( \Rightarrow \dfrac{{{{\rm{A}}^\prime }{\rm{E}}}}{{{\rm{AB}}}} = \dfrac{1}{3}\).
Theo định lí Talet \(\dfrac{{{{\rm{A}}^\prime }{\rm{E}}}}{{{\rm{AB}}}} = \dfrac{{{{\rm{A}}^\prime }{\rm{G}}}}{{{\rm{AG}}}} = \dfrac{1}{3} \Rightarrow \dfrac{{{\rm{GA}}}}{{{\rm{G}}{{\rm{A}}^\prime }}} = 3\).
Hướng dẫn giải:
Chứng minh \({A^\prime }E//AB\) sau đó áp dụng định lí Ta-lét.
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 3 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
