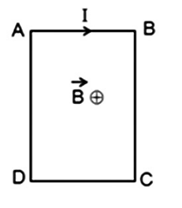
Một dây dẫn được uốn thành một khung dây có dạng hình tam giác vuông ABC như hình vẽ.
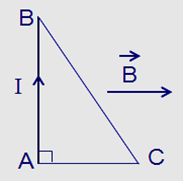
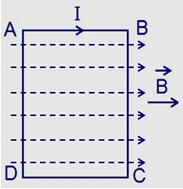
Đặt khung dây vào trong từ trường đều có véc tơ cảm ứng từ \(\mathop B\limits^ \to \) song song với cạnh AC. Coi khung dây nằm cố định trong mặt phẳng hình vẽ. Cho \(AB{\rm{ }} = 4{\rm{ }}cm\) , \(AC{\rm{ }} = 3cm\) , \(B{\rm{ }} = {\rm{ }}{5.10^{ - 3}}T\) ,\(I{\rm{ }} = {\rm{ }}5{\rm{ }}A\) . Lực từ tác dụng lên cạnh BC của khung dây có giá trị:
Trả lời bởi giáo viên
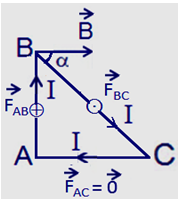
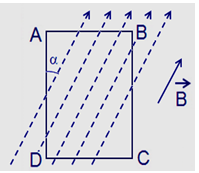
Lực từ tác dụng lên cạnh BC là \(\mathop {{F_{BC}}}\limits^ \to \) có điểm đặt tại trung điểm của BC, có phương vuông góc với mặt phẳng chứa khung dây, hướng từ trong ra ngoài và có độ lớn:
\({F_{BC}} = BI.BC.\sin \alpha \)
Xét \(\Delta ABC\), có:
\(\begin{array}{l}BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{4^2} + {3^2}} = 5cm\\\sin \widehat {ABC} = \dfrac{{AC}}{{BC}} = \dfrac{3}{5} = 0,6\\ \Rightarrow \widehat {ABC} = 36,{87^0}\\ \Rightarrow \alpha = {90^0} - \widehat {ABC} = 53,{13^0}\\ \Rightarrow \sin \alpha = 0,8\end{array}\)
\(\begin{array}{l} \Rightarrow {F_{BC}} = BI.BC.\sin \alpha \\ = {5.10^{ - 3}}.5.0,05.0,8 = {10^{ - 3}}N\end{array}\)
Hướng dẫn giải:
+ Vận dụng biểu thức tính tính lực từ: \(F = BIlsin\alpha \)
+ Sử dụng hệ thức lượng trong tam giác