Câu hỏi:
2 năm trước
Một con lắc đơn có chiều dài 0,8 m. Kéo lệch dây treo con lắc hợp với phương thẳng đứng góc 600 rồi thả nhẹ. Bỏ qua lực cản không khí. Lấy g = 10 m/s2. Chọn gốc thế năng tại vị trí thấp nhất của vật. Tính tốc độ cực đại của con lắc đạt được trong quá trình dao động.
Trả lời bởi giáo viên
Đáp án đúng: a
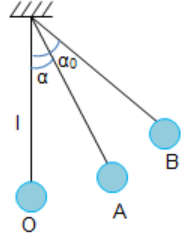
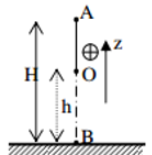
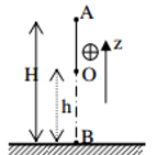
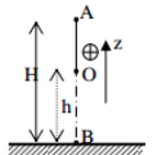
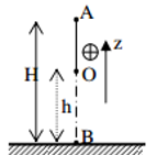
Chọn gốc thế năng tại O.
+ Cơ năng của vật tại O: \({{\rm{W}}_O} = {{\rm{W}}_{tO}} + {{\rm{W}}_{dO}} = \dfrac{1}{2}mv_{\max }^2\)
+ Cơ năng của vật tại B: \({{\rm{W}}_B} = {{\rm{W}}_{tB}} + {{\rm{W}}_{dB}} = mg.{z_B} = mg.l.\left( {1 - \cos {\alpha _0}} \right)\)
Áp dụng định luật bảo toàn cơ năng tại O và B ta có:
\(\begin{array}{l}{{\rm{W}}_O} = {{\rm{W}}_B} \Leftrightarrow \dfrac{1}{2}mv_{\max }^2 = mgl.\left( {1 - \cos {\alpha _0}} \right)\\ \Rightarrow {v_{\max }} = \sqrt {2gl.\left( {1 - \cos {\alpha _0}} \right)} = \sqrt {2.10.0,8.\left( {1 - \cos 60} \right)} = 2\sqrt 2 m/s\end{array}\)
Hướng dẫn giải:
Áp dụng định luật bảo toàn cơ năng.
Cơ năng của vật chuyển động trong trọng trường:\({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t}\)
