Câu hỏi:
2 năm trước
Một cây tre cau \(8m\) bị gió bão làm gãy ngang thân, ngọn cây chạm đất cách gốc \(3,5m\) . Hỏi điểm gãy cách gốc bao nhiêu? (làm tròn đến chữ số thập phân thứ hai)
Trả lời bởi giáo viên
Đáp án đúng: b
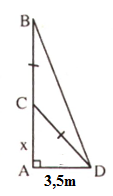
Giả sử \(AB\) là độ cao của cây tre, \(C\) là điểm gãy.
Đặt \(AC = x \Rightarrow CB = CD = 8-x\)
Vì \(\Delta ACD\) vuông tại \(A\)
\(⇒A{C^2} + A{D^2} = C{D^2}\)\( \Rightarrow {x^2} + 3,{5^2} = {\left( {8 - x} \right)^2}\)\( \Rightarrow 16x = \dfrac{{207}}{4} \)\(\Rightarrow x = \dfrac{{207}}{{64}} \approx 3,23m\)
Vậy điểm gãy cách gốc cây \(3,23\,m\)
Hướng dẫn giải:
Sử dụng định lý Py-ta-go trong tam giác vuông
Câu hỏi khác
- Đề kiểm tra 15 phút chương 5: hệ thức lượng trong tam giác vuông - đề số 1 Toán 9 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 5: hệ thức lượng trong tam giác vuông - đề số 2 Toán 9 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 5: hệ thức lượng trong tam giác vuông - đề số 1 Toán 9 có lời giải chi tiết
