Câu hỏi:
3 năm trước
Cho tam giác $ABC$ vuông tại $A$ có $AB = 21\,cm$; $\widehat C = 40^\circ $ , phân giác \(BD\) (\(D\) thuộc \(AC\) ). Độ dài phân giác $BD$ là (Kết quả làm tròn đến chữ số thập phân thứ nhất)
Trả lời bởi giáo viên
Đáp án đúng: d
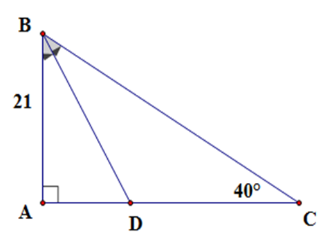
Xét tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ABC} + \widehat C = 90^\circ \Rightarrow \widehat {ABC} = 50^\circ \)
Mà \(BD\) là phân giác góc \(ABC\) nên \(\widehat {ABD} = \dfrac{1}{2}\widehat {ABC} = 25^\circ \)
Xét tam giác \(ABD\) vuông tại \(A\) ta có \(BD = \dfrac{{AB}}{{\cos \widehat {ABD}}} = \dfrac{{21}}{{\cos 25^\circ }} \approx 23,2\,cm\)
Hướng dẫn giải:
+ Tính góc \(ABC\) từ đó suy ra góc \(ABD\)
+ Sử dụng hệ thức về cạnh và góc trong tam giác vuông \(ABD\) để tính \(BD.\)

