Câu hỏi:
2 năm trước
Giải tam giác vuông $ABC,$ biết $\widehat A = 90^\circ \;$ và $BC = 50cm;\widehat B = {48^o}$ (làm tròn đến chữ số thập phân thứ nhất)
Trả lời bởi giáo viên
Đáp án đúng: d
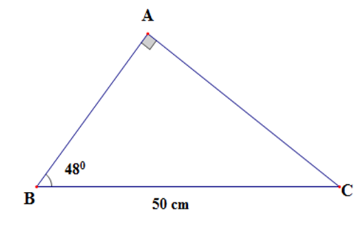
Xét $\Delta ABC$ có: $\widehat A = {90^o}$
$\widehat B + \widehat C = 90^\circ \Rightarrow \widehat C = 90^\circ - \widehat B = {90^o} - {48^o} = {42^o}$ ($\widehat C$ và $\widehat B$ là hai góc phụ nhau)
Áp dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông ta có:
\(AC = BC.\sin B = 50.\sin 48^\circ \approx 37,2cm\)
\(AB = BC.\cos B = 50.\cos 48^\circ \approx 33,5cm\)
Vậy \(AC = 37,2\,cm;\,AB = 33,5\,cm;\,\widehat C = 42^\circ \) .
Hướng dẫn giải:
Giải tam giác vuông là tìm tất cả các cạnh và góc của tam giác vuông đó
Sử dụng các tỉ số lượng giác, định lý về góc trong tam giác, hệ thức liên hệ giữa cạnh và góc trong tam giác vuông.
Câu hỏi khác
- Đề kiểm tra 15 phút chương 5: hệ thức lượng trong tam giác vuông - đề số 1 Toán 9 có lời giải chi tiết
- Đề kiểm tra 15 phút chương 5: hệ thức lượng trong tam giác vuông - đề số 2 Toán 9 có lời giải chi tiết
- Đề kiểm tra 45 phút chương 5: hệ thức lượng trong tam giác vuông - đề số 1 Toán 9 có lời giải chi tiết
