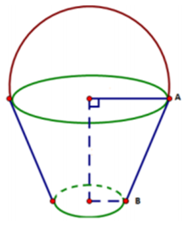
Một cái xô bằng inox có dạng như hình vẽ. Đáy trên có đường kính \(42\;{\rm{cm}}\), đáy dưới có đường kính \(18\;{\rm{cm}}\), cạnh bên \(AB = 36\;{\rm{cm}}\). Tính diện tích xung quanh của cái xô.
Trả lời bởi giáo viên
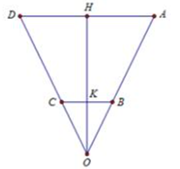
\(\begin{array}{l}\dfrac{{OB}}{{OA}} = \dfrac{{BC}}{{AD}} \Leftrightarrow \dfrac{{OB}}{{OB + 36}} = \dfrac{{18}}{{42}}\\ \Rightarrow OB = 27 \Rightarrow OA = 27 + 36 = 63\end{array}\)
Diện tích xung quanh của hình nón đỉnh \({\rm{O}}\) đáy là hình tròn lớn là
\({S_1} = \pi {R_1}.OA = \pi (42:2) \cdot 63 = 1323\pi \)
Diện tích xung quanh của hình nón đỉnh \(O\) đáy là hình tròn nhỏ là :
\({{\rm{S}}_2} = \pi {{\rm{R}}_2} \cdot {\rm{OB}} = \pi (18:2).27 = 243\pi \)
Diện tích xung quanh của cái xô là :
\({{\rm{S}}_{{\rm{xq}}}} = {{\rm{S}}_1} - {{\rm{S}}_2} = 1323\pi - 243\pi = 1080\pi \)
Hướng dẫn giải:
Diện tích xung quanh của cái xô = Diện tích xung quanh của hình nón đỉnh \({\rm{O}}\) đáy là hình tròn lớn - Diện tích xung quanh của hình nón đỉnh \(O\) đáy là hình tròn nhỏ.


