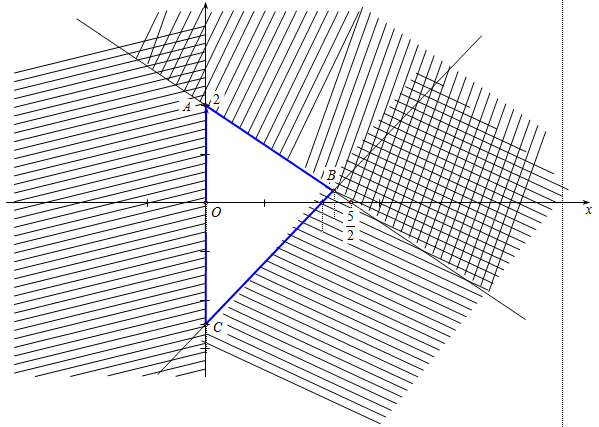
Miền tam giác \(ABC\) kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn bệ A, B, C, D ?
Trả lời bởi giáo viên
Dựa vào hình vẽ, ta thấy:
Đường thẳng \(\left( {{d_1}} \right)\) là trục tung Oy nên có phương trình x=0.
Đường thẳng \(\left( {{d_2}} \right)\) đi qua hai điểm (0;2) và \((\dfrac{5}{2};0)\) nên có phương trình \(\frac{x}{{\frac{5}{2}}} + \frac{y}{2} = 1 \Leftrightarrow \frac{{2x}}{5} + \frac{y}{2} = 1 \Leftrightarrow 4x + 5y = 10\)
Đường thẳng \(\left( {{d_3}} \right)\) đi qua các điểm (2;0) và \((0;-\dfrac{5}{2})\) nên có phương trình \(\frac{x}{2} + \frac{y}{{ - \frac{5}{2}}} = 1 \Leftrightarrow \frac{x}{2} - \frac{{2y}}{5} = 1 \Leftrightarrow 5x - 4y = 10\)
Miền nghiệm gần phần mặt phẳng nhận giá trị \(x\) dương (kể cả bờ \(\left( {{d_1}} \right)\)).
Lại có \(\left( {0\,\,;\,\,0} \right)\) là nghiệm của cả hai bất phương trình \(4x + 5y \le 10\) và \(5x - 4y \le 10.\)
Vậy miền tam giác ABC biểu diễn nghiệm của hệ câu C.
Hướng dẫn giải:
- Tìm phương trình các đường thẳng giới hạn miền nghiệm.
- Kiểm tra điểm thuộc miền nghiệm và kết luận.
Giải thích thêm:
Một số em có thể sẽ chọn nhầm đáp án D vì không để ý miền nghiệm có cả 3 cạnh nên \(\left( {0;0} \right)\) vẫn thuộc miền nghiệm.


