Mặt cầu $\left( S \right)$ có tâm \(I( - 1;2; - 5)\) cắt mặt phẳng \(\left( P \right):2x - 2y - z + 10 = 0\) theo thiết diện là hình tròn có diện tích \(3\pi \). Phương trình của $\left( S \right)$ là:
Trả lời bởi giáo viên
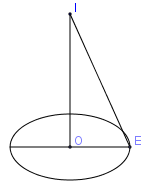
Gọi $O$ là tâm của đường tròn thiết diện, $E$ là một điểm thuộc đường tròn.
Ta có: $IO = d\left( {I,(P)} \right);R = IE$
\(IO = d\left( {I,(P)} \right) = \dfrac{{|2.( - 1) - 2.2 + 5 + 10|}}{{\sqrt {{2^2} + {2^2} + 1} }} = 3\)
\(S = 3\pi = \pi .O{E^2} \Leftrightarrow O{E^2} = 3\)
Tam giác $IOE$ vuông tại $O$ nên \({R^2} = I{E^2} = I{O^2} + O{E^2} = 3 + 9 = 12.\)
Suy ra phương trình mặt cầu $\left( S \right)$ là:
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 5} \right)^2} = 12\) hay \({x^2} + {y^2} + {z^2} + 2x - 4y + 10z + 18 = 0\)
Hướng dẫn giải:
+ Xác định bán kính mặt cầu $\left( S \right)$
+ Phương trình mặt cầu: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)

