Câu hỏi:
2 năm trước
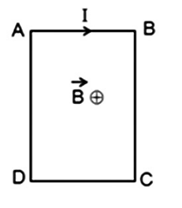
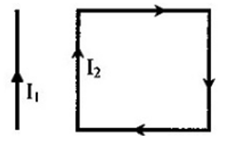
Khung dây hình vuông ABCD có cạnh a = 4cm, dòng điện I2 = 20A đi qua, một dòng điện thẳng I1 = 15A nằm trong mặt phẳng ABCD cách AD một khoảng d = 2cm như hình vẽ.
Lực từ tổng hợp do I1 tác dụng lên khung dây có giá trị là:
Trả lời bởi giáo viên
Đáp án đúng: b
+ Từ trường do dòng I1 gây nên tại các vị trí nằm trên cạnh khung dây có chiều hướng vào mặt phẳng hình vẽ:
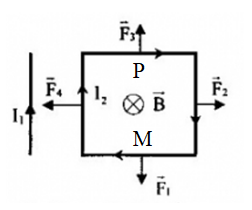
+ Lực từ tác dụng lên mỗi cạnh của khung dây được xác định theo quy tắc bàn tay trái
+ Các lực từ nói trên nằm trong mặt phẳng khung dây nên không gây ra momen làm cho khung quay
+ Hợp lực tác dụng lên khung dây: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} \)
+ Do tính chất đối xứng nên cảm ứng từ do I1 gây nên tại M và P bằng nhau, nên F1 và F3 trực đối
\( \to \overrightarrow {{F_1}} + \overrightarrow {{F_3}} = 0\)
+Vậy hợp lực: \(\overrightarrow F = \overrightarrow {{F_2}} + \overrightarrow {{F_4}} \)
Ta có: \(\left\{ \begin{array}{l}{F_2} = {2.10^{ - 7}}\frac{{{I_1}{I_2}}}{{d + a}}a = {4.10^{ - 5}}(N)\\{F_3} = {2.10^{ - 7}}\frac{{{I_1}{I_2}}}{d}a = {12.10^{ - 5}}(N)\end{array} \right.\)
Mặt khác, \(\overrightarrow {{F_2}} \uparrow \downarrow \overrightarrow {{F_4}} \to F = {F_4} - {F_2} = {12.10^{ - 5}} - {4.10^{ - 5}} = {8.10^{ - 5}}(N)\)
Hướng dẫn giải:
+ Áp dụng quy tắc bàn tay trái, xác định chiều lực từ
+ Vận dụng biểu thức tính tính lực từ gây ra bởi dòng điện thẳng dài: \(F = {2.10^{ - 7}}\frac{{{I_1}{I_2}}}{r}\)
+ Vận dụng biểu thức tính tính lực từ: \(F = BIlsin\alpha \)
Câu hỏi khác
- Bài tập từ trường của dòng điện trong các dây dẫn có hình dạng đặc biệt có lời giải MÔN LÝ lớp 11
- Bài tập lực từ - bài tập lực từ tác dụng lên đoạn dây dẫn mang điện lý 11 có lời giải
- Bài tập tương tác giữa hai dòng điện song song lý 11 có lời giải
- Bài tập khung dây đặt trong từ trường đều lý 11 có lời giải
- Bài tập từ trường lý 11 có lời giải
