Câu hỏi:
2 năm trước
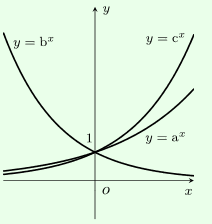
Hàm số nào sau đây nghịch biến trên \(\left( { - \infty ; + \infty } \right)\)?
Trả lời bởi giáo viên
Đáp án đúng: c
Do \(0 < \dfrac{2}{e} < 1\) nên hàm số y =\({\left( {\dfrac{2}{e}} \right)^x}\) nghịch biến trên \(\left( { - \infty ; + \infty } \right)\).
Hướng dẫn giải:
Hàm số \(y = {a^x}\,\,\,\left( {0 < a \ne 1} \right)\) nghịch biến trên \(\left( { - \infty ; + \infty } \right) \Leftrightarrow 0 < a < 1\).