Câu hỏi:
2 năm trước
Hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) có bảng biến thiên như sau:
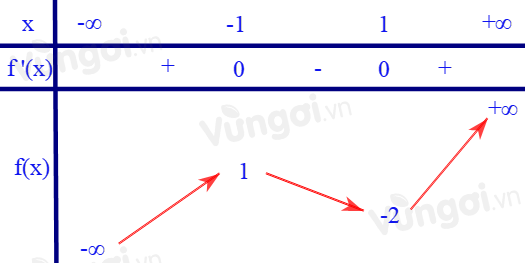
Số nghiệm của phương trình \(f\left( {{x^2} - x} \right) = 2\) là:
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đáp án:
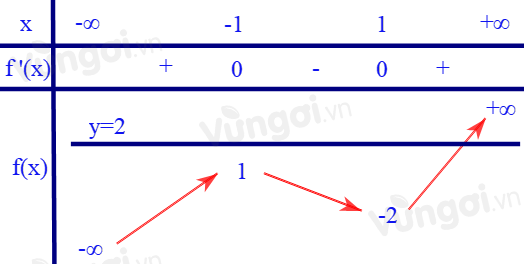
Từ bảng biến thiên ta có: \(f\left( {{x^2} - x} \right) = 2 \Leftrightarrow {x^2} - x = a \in \left( {1; + \infty } \right)\)
\(\begin{array}{l}{x^2} - x = a \Leftrightarrow {x^2} - x - a = 0\\\Delta = 1 + 4a > 0\end{array}\)
(Vì a>1)
=> phương trình \({x^2} - x - a = 0\) có 2 nghiệm phân biệt.
Vậy phương trình đã cho có 2 nghiệm phân biệt.
Hướng dẫn giải:
- Từ bảng biến thiên tìm \({x^2} - x\)
- Tìm số nghiệm x của phương trình \({x^2} - x = a\)


