Hai đại biểu của trường A và trường B tham dự một buổi hội thảo. Mỗi đại biểu của trường A lân lượt bắt tay với từng đại biểu của trường B một lần. Tính số đại biểu của mỗi trường, biết số cái bắt tay bằng ba lần tổng số đại biểu của cả hai trường và số đại biểu của trường A nhiều hơn số đại biểu của trường B.
Trả lời bởi giáo viên
Gọi số đại biểu của trường A là \(x\) (đại biểu) và số đại biểu của trường B là \(y\) (đại biểu) \(\left( {x,y \in \mathbb{N}^*;x > y} \right)\).
Mỗi đại biểu của trường A bắt tay với lần lượt từng đại biểu của trường B nên số cái bắt tay là \(xy\).
Vì số cái bắt tay bằng 3 lần tổng số đại biểu của cả hai trường nên \(xy = 3\left( {x + y} \right)\)
\( \Rightarrow xy = 3x + 3y \Leftrightarrow x\left( {y - 3} \right) = 3y\)
TH1: \(y = 3 \Leftrightarrow x.0 = 9\) (vô lí)
TH2: \(y \ne 3 \Rightarrow y = \dfrac{{3y}}{{y - 3}} = \dfrac{{3y - 9 + 9}}{{y - 3}} = 3 + \dfrac{9}{{y - 3}}\)
Do \(x \in \mathbb{N}^* \Rightarrow y - 3 \in Ư\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\)
Ta có bảng sau:
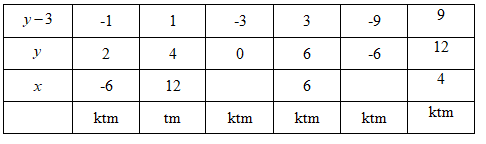
Vậy số đại biểu của trường A là 12 đại biểu và số đại biểu của trường B là 4 đại biểu.
Hướng dẫn giải:
Gọi số đại biểu của trường A là \(x\) (đại biểu) và số đại biểu của trường B là \(y\) (đại biểu) \(\left( {x,y \in \mathbb{N}*;x > y} \right)\).
Từ đó biểu diễn số cái bắt tay của các đại biểu hai trường.
Dựa vào điều kiện \(x,y \in \mathbb{N}*;x > y\) để biện luận và tìm số đại biểu các trường.

