Câu hỏi:
1 năm trước
Giá trị nhỏ nhất của biết thức $F = y - x$ trên miền xác định bởi hệ $\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.$ là.
Trả lời bởi giáo viên
Đáp án đúng: a
Biểu diễn miền nghiệm của hệ bất phương trình $\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.$ trên hệ trục tọa độ như dưới đây:
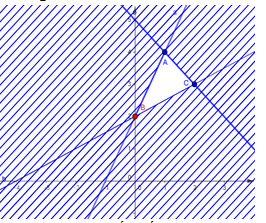
Nhận thấy biết thức $F = y - x$ chỉ đạt giá trị nhỏ nhất tại các điểm \(A,B\) hoặc \(C\).
Ta có: \(F\left( A \right) = 4 - 1 = 3;\,F\left( B \right) = 2;\,F\left( C \right) = 3 - 2 = 1\).
Vậy ${\rm{min }}F = 1$ khi $x = 2,y = 3$.
Hướng dẫn giải:
- Biểu diễn miền nghiệm của hệ bất phương trình trên hệ tọa độ.
- Biểu thức \(F\left( {x;y} \right)\) đạt max hoặc min chỉ tại một trong các điểm đầu mút nên ta chỉ cần tính giá trị của \(F\left( {x;y} \right)\) tại một trong các điểm đó.
Câu hỏi khác
- Đề thi kiểm tra giữa học kì 1 - Đề số 1 Toán 10 sách Kết nối tri thức với cuộc sống có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 5 Toán 10 sách Kết nối tri thức với cuộc sống có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 2 Toán 10 sách Kết nối tri thức với cuộc sống có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 3 Toán 10 sách Kết nối tri thức với cuộc sống có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 4 Toán 10 sách Kết nối tri thức với cuộc sống có lời giải chi tiết
