Trả lời bởi giáo viên
Đáp án đúng: a
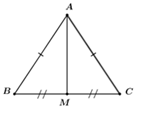
Xét tam giác \(ABC\) đều cạnh \(AB = BC = AC = a\) có \(AM\) là đường trung tuyến suy ra \(AM\) cũng là đường cao của tam giác \(ABC\) hay \(AM \bot BC\) tại \(M\).
Ta có \(MB = MC = \dfrac{{BC}}{2} = \dfrac{a}{2}\)
Xét tam giác $AMC$ vuông tại \(M\), theo định lý Pytago ta có
\(A{M^2} = A{C^2} - M{C^2} = {a^2} - {\left( {\dfrac{a}{2}} \right)^2}\)\( = {a^2} - \dfrac{{{a^2}}}{4} = \dfrac{{3{a^2}}}{4}\)
Vậy bình phương độ dài đường cao của tam giác đều cạnh \(a\) là \(\dfrac{{3{a^2}}}{4}.\)
Hướng dẫn giải:
Áp dụng tính chất tam giác đều, định lý py-ta-go.

