Trả lời bởi giáo viên
Đáp án đúng: d
Ta có sơ đồ:
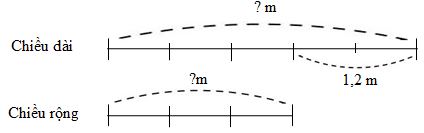
Theo sơ đồ, hiệu số phần bằng nhau là:
\(5 - 3 = 2\) (phần)
Giá trị một phần là:
\(1,2:2 = 0,6\;(m)\)
Chiều dài của cái thùng sắt đó là:
\(0,6 \times 5 = 3\;(m)\)
Chiều rộng của cái thùng sắt đó là:
\(3 - 1,2 = 1,8\;(m)\)
Diện tích xung quanh của thùng sắt đó là:
\((3 + 1,8) \times 2 \times 0,5 = 4,8\;({m^2})\)
Diện tích đáy của thùng sắt đó là:
\(3 \times 1,8 = 5,4\;({m^2})\)
Diện tích cần sơn là:
\((4,8 + 5,4) \times 2 = 20,4\;({m^2})\)
Đáp số: \(20,4{m^2}\).
Hướng dẫn giải:
Vì người đó muốn sơn cả mặt trong và mặt ngoài của thùng sắt không nắp nên diện tích cần sơn bằng hai lần tổng diện tích xung quanh và diện tích một mặt đáy.
Để giải bài này ta có thể làm như sau:
- Tìm chiều dài và chiều rộng của hình hộp chữ nhật theo dạng toán hiệu – tỉ cơ bản đã học.
- Tính diện tích xung quanh của thùng sắt ta lấy chu vi đáy nhân với chiều cao.
- Tính diện tích đáy của thùng sắt ta lấy chiều dài nhân với chiều rộng.
- Tính diện tích cần sơn khi sơn mặt trong và mặt ngoài cái thùng đó ta lấy tổng diện tích xung quanh của thùng cộng với diện tích đáy rồi nhân với \(2\).
Câu hỏi khác
Câu 7:
199
