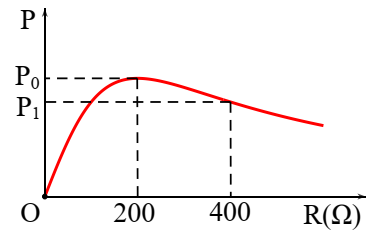
Đặt vào hai đầu đoạn mạch RLC một điện áp xoay chiều. Thay đổi R ta thu được đồ thị biểu diễn công suất tiêu thụ của mạch điện như hình vẽ. Quan hệ giữa \({P_1}\) và \({P_0}\) là
Trả lời bởi giáo viên
Từ đồ thị ta có:
+ Tại \(R = 200\Omega \) công suất của mạch cực đại khi đó
\({P_{\max }} = {P_0} = \dfrac{{{U^2}}}{{2R}} = \dfrac{{{U^2}}}{{2.200}} = \dfrac{{{U^2}}}{{400}}\,\,\left( 1 \right)\) và \(R = \left| {{Z_L} - {Z_C}} \right| = 200\Omega \)
+ Tại \(R = 400\Omega \) công suất của mạch khi đó:
\(P = \dfrac{{{U^2}}}{{{Z^2}}}R = \dfrac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R\)
\( \Rightarrow P = \dfrac{{{U^2}}}{{{{400}^2} + {{200}^2}}}.400 = \dfrac{{{U^2}}}{{500}}\,\,\,\left( 2 \right)\)
+ Từ (1) và (2) ta suy ra:
\(\dfrac{{{P_1}}}{{{P_0}}} = \dfrac{{\dfrac{{{U^2}}}{{500}}}}{{\dfrac{{{U^2}}}{{400}}}} = \dfrac{4}{5} \Rightarrow {P_1} = \dfrac{4}{5}{P_0}\)
Hướng dẫn giải:
Đọc đồ thị và khai thác thông tin từ đồ thị.
Công thức tính công suất: \(P = UI.\cos \varphi = \dfrac{{{U^2}}}{{{Z^2}}}R\)
Bài toán R thay đổi để công suất cực đại: \({P_{\max }} = \dfrac{{{U^2}}}{{2R}};R = \left| {{Z_L} - {Z_C}} \right|\)
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 3 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
