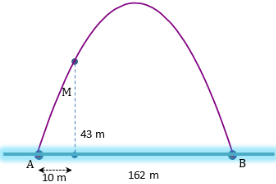
Cổng Ac-xơ tại thành phố Xanh Lu-i (Mĩ) có hình dạng là một parabol hướng bề lõm xuống dưới (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính chiều cao (mét) của cổng Ac-xơ (làm tròn đến hàng đơn vị)
Chỉ điền các số nguyên, phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
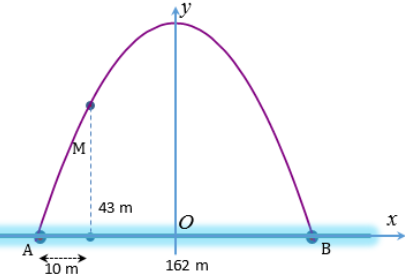
Ta chọn hệ trục Oxy như hình vẽ.
AB=162(m) nên \({x_B} = \dfrac{{162}}{2} = 81\)
\({x_M} = - \left( {OA - 10} \right) = - \left( {81 - 10} \right) = - 71\)
Vì Parabol đối xứng qua Oy nên có phương trình dạng: \(y = a{x^2} + c\left( {a < 0} \right)\)
Parabol đi qua điểm \(B\left( {81;0} \right)\) và \(M\left( { - 71;43} \right)\) nên ta có hệ:
\(\left\{ \begin{array}{l}0 = a{.81^2} + c\\43 = a.{\left( { - 71} \right)^2} + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{{43}}{{1520}}\\c = \dfrac{{282123}}{{1520}}\end{array} \right.\)
Chiều cao của cổng Ac-xơ là:
\(h = y\left( 0 \right) = c = \dfrac{{282123}}{{1520}} \approx 186\left( m \right)\)
Hướng dẫn giải:
Gắn hệ trục tọa độ cho hình vẽ.
Viết phương trình của Parabol.
Thay tọa độ điểm B và điểm M vào phương trình rồi tìm c, giá trị gần đúng của c là số cần tìm.
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
