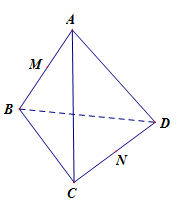
Cho tứ diện đều \(ABCD\),\(M\) và \(N\) theo thứ tự là trung điểm của cạnh \(AB\) và \(CD\). Mệnh đề nào sau đây sai?

A.Đúng vì:  \(\overrightarrow {AC}  + \overrightarrow {BD}  = \left( {\overrightarrow {AD}  + \overrightarrow {DC} } \right) + \left( {\overrightarrow {BC}  + \overrightarrow {CD} } \right) = \overrightarrow {AD}  + \overrightarrow {BC} \)

B. Đúng vì: \(\overrightarrow {AD}  + \overrightarrow {BC}  = \left( {\overrightarrow {AM}  + \overrightarrow {MN}  + \overrightarrow {ND} } \right) + \left( {\overrightarrow {BM}  + \overrightarrow {MN}  + \overrightarrow {NC} } \right)\)\( = 2\overrightarrow {MN}  + \left( {\overrightarrow {AM}  + \overrightarrow {BM} } \right) + \left( {\overrightarrow {ND}  + \overrightarrow {NC} } \right) = 2\overrightarrow {MN} \)

C.Đúng vì:  \(\overrightarrow {AC}  + \overrightarrow {BD}  + \overrightarrow {AD}  + \overrightarrow {BC}  = 2\overrightarrow {AN}  + 2\overrightarrow {BN}  = 2\left( {\overrightarrow {AN}  + \overrightarrow {BN} } \right) =  - 2\left( {\overrightarrow {NA}  + \overrightarrow {NB} } \right) =  - 4\overrightarrow {NM} \)

Vậy D sai.