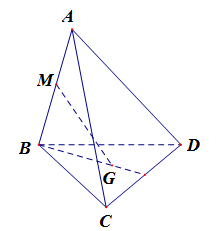
Cho tứ diện đều \(ABCD\),\(M\) là trung điểm của cạnh \(AB\) và \(G\) là trọng tâm cảu tam giác \(BCD\). Đặt \(\overrightarrow {AB}  = \overrightarrow b ,\overrightarrow {AC}  = \overrightarrow c ,\overrightarrow {AD}  = \overrightarrow d \). Phân tích véc tơ \(\overrightarrow {MG} \) theo \(\overrightarrow d ,\overrightarrow b ,\overrightarrow c \) .

\(\overrightarrow {AC}  + \overrightarrow {BD}  = \overrightarrow {AD}  + \overrightarrow {BC} \) 

\(\overrightarrow {MN}  = \dfrac{1}{2}\left( {\overrightarrow {AD}  + \overrightarrow {BC} } \right)\)

\(\overrightarrow {AC}  + \overrightarrow {BD}  + \overrightarrow {AD}  + \overrightarrow {BC}  =  - 4\overrightarrow {NM} \).

\(\overrightarrow {MC}  + \overrightarrow {MD}  - 4\overrightarrow {MN}  = \overrightarrow 0 \).

$0.$

$ - \dfrac{1}{2}.$

$ - \dfrac{1}{{\sqrt 2 }}.$     

$\dfrac{1}{{\sqrt 2 }}.$

\(H\) là trực tâm \(\Delta ABC\).

\(H\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).

\(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\)

\(CH\) là đường cao của \(\Delta ABC\).

vuông góc với hai đường thẳng phân biệt nằm trong mp \(\left( P \right).\)

vuông góc với đường thẳng \(a\) mà $a$ song song với mp \(\left( P \right)\) 

vuông góc với đường thẳng \(a\) nằm trong mp \(\left( P \right).\)

vuông góc với mọi đường thẳng nằm trong mp \(\left( P \right).\)

$ - 3;1;5;9;14$            

$5;2; - 1; - 4; - 7$       

\(\dfrac{5}{3},1,\dfrac{1}{3}, - \dfrac{1}{3}, - 3\)

\( - \dfrac{7}{2}, - \dfrac{5}{2}, - 2; - \dfrac{1}{2};\dfrac{1}{2}\)

Hình thang cân

Hình thang vuông

Hình chữ nhật

Hình vuông

$12$  

$13$  

$14$  

$15$