Câu hỏi:
3 năm trước
Cho tứ diện $ABCD.$ Gọi $M, N, P, Q$ lần lượt là trung điểm của các cạnh $AB, AD, CD, BC.$ Mệnh đề nào sau đây là sai ?
Trả lời bởi giáo viên
Đáp án đúng: a
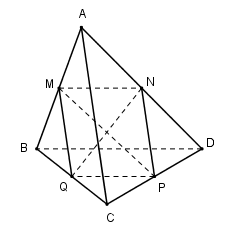
Ta có: $MN, PQ$ lần lượt là đường trung bình của tam giác $ABD$ và $CBD$ nên
$MN // BD ;$ \(MN = \dfrac{1}{2}BD\) và $ PQ // BD ;$ \(PQ = \dfrac{1}{2}BD\)
\( \Rightarrow \) $MN // PQ$ và $MN = PQ$
Do đó $MNPQ $ là hình bình hành nên $MP,NQ$ cùng thuộc một mặt phẳng.
Vậy A sai.
Hướng dẫn giải:
- Đưa về cùng mặt phẳng.
- Sử dụng các tính chất đường trung bình của tam giác.