Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) có \(AC = 3cm\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(C\) kẻ \(CM{\rm{//}}xy\left( {M \in AB} \right)\) . Chọn câu đúng.
Trả lời bởi giáo viên
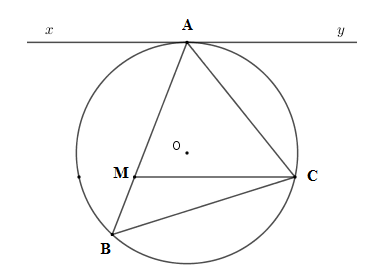
Ta có \(\widehat {yAC} = \widehat {ABC}\) (hệ quả góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\) ) mà \(\widehat {yAC} = \widehat {ACM}\) (so le trong) nên \(\widehat {ABC} = \widehat {ACM} \Rightarrow \Delta AMC\backsim\Delta ACB\left( {g - g} \right)\)
\(\dfrac{{AM}}{{AC}} = \dfrac{{AC}}{{AB}} \Rightarrow AM.AB = A{C^2} = {3^2} = 9\left( {c{m^2}} \right)\) .
Hướng dẫn giải:
Sử dụng hệ quả về góc tạo bởi tiếp tuyến và dây cung: “ Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau” để chứng minh các góc bằng nhau
Từ đó suy ra tam giác đồng dạng theo trường hợp góc-góc và suy ra hệ thức tương ứng.

