Câu hỏi:
2 năm trước
Cho tam giác $MNP$ có $MN = MP.$ Gọi $A$ là trung điểm của $NP.$ Biết \(\widehat {NMP} = {40^0}\) thì số đo góc $MPN$ là:
Trả lời bởi giáo viên
Đáp án đúng: b
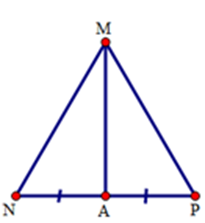
Xét tam giác $NAM$ và tam giác $PAM$ có:
$MN = MP,$ $NA = PA,$ $MA$ là cạnh chung. Do đó \(\Delta NAM = \Delta PAM\,\left( {c - c - c} \right).\)
Suy ra \(\widehat {ANM} = \widehat {APM}\) (hai góc tương ứng),
Ta có \(\widehat {ANM} = \widehat {APM}\)(cmt). Xét tam giác $MNP$ có:
\(\widehat {NMP} + \widehat {MPN} + \widehat {PNM} = {180^0} \Rightarrow 2\widehat {MPN} + \widehat {NMP} = {180^0}\)
\(\widehat {MPN} = \left( {{{180}^0} - \widehat {NMP}} \right):2 = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}.\)
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
