Câu hỏi:
1 năm trước
Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M, N sao cho BM = CN = AB. Tính \(\widehat {MAN}\).
Trả lời bởi giáo viên
Đáp án đúng: b
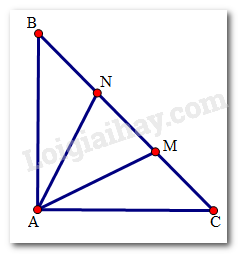
Do tam giác ABC vuông cân ở A nên \(\widehat B = \widehat C = {45^0}\).
Xét tam giác AMB có: BM = BA (gt), nên tam giác AMB cân ở B.
Do đó \(\widehat {AMB} = \frac{{{{180}^0} - \widehat B}}{2} = \frac{{{{180}^0} - {{45}^0}}}{2} = 67,5^\circ \)
Chứng minh tương tự ta được tam giác ANC cân ở C và \(\widehat {ANC} = 67,5^\circ \).
Xét tam giác AMN, ta có:
\(\widehat {MAN} = {180^0} - \left( {\widehat {AMN} + \widehat {ANM}} \right) = {180^0} - {135^0} = {45^0}\).
Vậy \(\widehat {MAN} = {45^0}\)
Hướng dẫn giải:
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân, tính được \(\widehat {ANM},\widehat {AMN}\) suy ra số đo góc MAN
Câu hỏi khác
- Bài tập trắc nghiệm Tổng các góc trong một tam giác môn Toán lớp 7 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác môn Toán lớp 7 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Các trường hợp bằng nhau của tam giác vuông môn Toán lớp 7 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác môn Toán lớp 7 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Tam giác cân. Đường trung trực của đoạn thẳng môn Toán lớp 7 sách KNTTVCS có lời giải
