Câu hỏi:
3 năm trước
Cho tam giác \(ABC\) nhọn nội tiếp \(\left( O \right)\). Hai đường cao \(BD\) và \(CE\) cắt nhau tại \(H\). Vẽ đường kính \(AF\) .
Hai đoạn thẳng nào sau đây bằng nhau?
Trả lời bởi giáo viên
Đáp án đúng: c
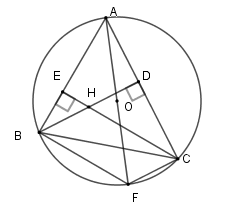
Xét \(\left( O \right)\) có \(\widehat {ACF} = 90^\circ ;\widehat {ABF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Suy ra \(CF \bot AC;BF \bot AB\) mà $BD \bot AC;CE \bot AB$\( \Rightarrow BD{\rm{//}}CF;CE{\rm{//}}BF\)
$ \Rightarrow BHCF$ là hình bình hành
\( \Rightarrow BH = CF;BF = CH\) .
Hướng dẫn giải:
+ Sử dụng hệ quả của góc nội tiếp để chứng minh các đường thẳng song song
+ Từ đó chứng minh \(BHCF\) là hình bình hành và suy ra các đoạn thẳng bằng nhau

