Cho tam giác $ABC$ đều cạnh bằng $1$. Tính \(\overrightarrow {AB} .\overrightarrow {BC} \) ?
Trả lời bởi giáo viên
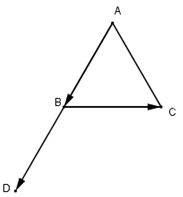
Lấy điểm $D$ sao cho \(\overrightarrow {AB} = \overrightarrow {BD} \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {BD} ;\overrightarrow {BC} } \right) = {120^0}\)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {BC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = 1.1.\cos {120^0} = - \dfrac{1}{2}\)
(vì tam giác $ABC$ đều cạnh $1$ nên \(AB = BC = 1 \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right| = 1\))
Hướng dẫn giải:
- Sử dụng định nghĩa tích vô hướng của 2 vectơ \(\overrightarrow u ,\overrightarrow v \) là \(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\cos \left( {\overrightarrow u ,\overrightarrow v } \right)\).
- Sử dụng công thức \(AB = \left| {\overrightarrow {AB} } \right|\).
- Lưu ý khi xác định góc giữa hai vectơ: Muốn xác định góc giữa hai vectơ phải đưa về 2 vectơ chung điểm đầu.

