Cho hình vuông \(ABCD\) có tâm là \(O\) và cạnh \(a\). \(M\) là một điểm bất kỳ. Chứng minh rằng \(\overrightarrow u = \overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} - \overrightarrow {MD} \) không phụ thuộc vị trí điểm \(M\). Tính độ dài vectơ \(\overrightarrow u \)
Trả lời bởi giáo viên
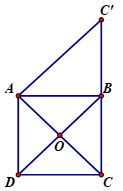
Theo quy tắc phép trừ ta có
\(\overrightarrow u = \left( {\overrightarrow {MA} - \overrightarrow {MC} } \right) + \left( {\overrightarrow {MB} - \overrightarrow {MD} } \right) = \overrightarrow {CA} + \overrightarrow {DB} \)
Suy ra \(\overrightarrow u \) không phụ thuộc vị trí điểm \(M\).
Qua \(A\) kẻ đường thẳng song song với \(DB\) cắt \(BC\) tại \(C'\).
Khi đó tứ giác \(ADBC'\) là hình bình hành (vì có cặp cạnh đối song song) suy ra \(\overrightarrow {DB} = \overrightarrow {AC'} \)
Do đó \(\overrightarrow u = \overrightarrow {CA} + \overrightarrow {AC'} = \overrightarrow {CC'} \)
=> \(\left| {\overrightarrow u } \right| = \left| {\overrightarrow {CC'} } \right| =CC'= BC + BC' \)
Mà ta có $BC'=AD=a$ (do $ADBC'$ là hình bình hành) và $BC=a$ (gt)
Vậy \(\left| {\overrightarrow u } \right| = a + a = 2a\)
Hướng dẫn giải:
- Sử dụng quy tắc ba điểm, trừ hai véc tơ tính \(\overrightarrow u \) mà không có xuất hiện điểm \(M\) trong biểu thức tính của véc tơ \(\overrightarrow u \)
- Tính độ dài của véc tơ \(\overrightarrow u \)

