Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có ba góc nhọn, đường cao $AH$ và nội tiếp đường tròn tâm $(O)$, đường kính $AM$
Góc $\widehat {OAC}$ bằng
Trả lời bởi giáo viên
Đáp án đúng: b
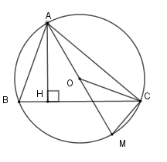
Xét \(\left( O \right)\) có \(\widehat {ABC}\) là góc nội tiếp chắn cung \(AC\) và \(\widehat {CAM}\) là góc nội tiếp chắn cung \(CM\)
Nên \(\widehat {ABC} = \dfrac{1}{2}\) sđ \(\overparen{AC}\) ;
\(\widehat {CAM} = \dfrac{1}{2}\) sđ \(\overparen{CM}\)
Lại có sđ \(\overparen{AC}+\) sđ \(\overparen{CM}= 180^\circ \) nên \(\widehat {ABC} + \widehat {CAM} = \dfrac{{180^\circ }}{2} = 90^\circ \)
Mà \(\widehat {ABC} + \widehat {ABH} = 90^\circ \) nên \(\widehat {ABH} = \widehat {CAM}\) .
Hướng dẫn giải:
Sử dụng số đo của góc nội tiếp bằng nửa số đo cung bị chắn

