Cho tam giác \(ABC\) có \(AH \bot BC\) và \(\widehat {BAH} = 2.\widehat C\) . Tia phân giác của góc \(B\) cắt \(AC\) ở \(E.\) Tia phân giác của góc \(BAH\) cắt \(BE\) ở \(I.\) Khi đó tam giác \(AIE\) là tam giác

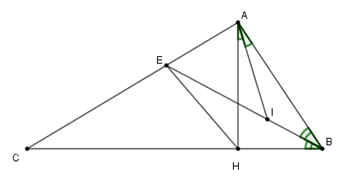
Xét tam giác \(AHB\) vuông ta có \(\widehat {BAH} + \widehat {ABH} = 90^\circ \) mà  \(\widehat {BAH} = 2\widehat C\) và \(\widehat {ABH} = 2.\widehat {IBH}\)

Suy ra \(2\widehat C + 2.\widehat {IBH} = 90^\circ  \Rightarrow 2\left( {\widehat C + \widehat {IBH}} \right) = 90^\circ \) \( \Rightarrow \widehat C + \widehat {EBH} = 45^\circ \) .

Xét tam giác \(BEC\) có \(\widehat {IEA}\) là góc ngoài tại đỉnh \(E\) nên \(\widehat {AEI} = \widehat {ECB} + \widehat {EBC} = 45^\circ \)

Xét tam giác \(AHB\) có  \(\widehat {BAH} + \widehat {HBA} = 90^\circ  \Rightarrow 2.\widehat {IAB} + 2.\widehat {IBA} = 90^\circ \)\( \Rightarrow \widehat {IAB} + \widehat {IBA} = 90^\circ :2\)

\( \Rightarrow \widehat {IAB} + \widehat {IBA} = 45^\circ \)

Xét tam giác \(AIB\) có \(\widehat {AIE}\) là góc ngoài tại đỉnh \(I\) nên \(\widehat {AIE} = \widehat {IAB} + \widehat {IBA} = 45^\circ \)

Xét tam giác \(IAE\) có \(\widehat {AIE} = 45^\circ  = \widehat {AEI}\)  suy ra \(\widehat {EAI} = 180^\circ  - \widehat {AEI} - \widehat {AIE} = 90^\circ \) (tổng ba góc trong tam giác)

Nên tam giác \(IAE\) vuông cân tại \(A.\)