Cho tam giác $ABC$ cân tại $A$; đường cao $AH$ và $BK$ cắt nhau tại $I$. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính $AI$.
Trả lời bởi giáo viên
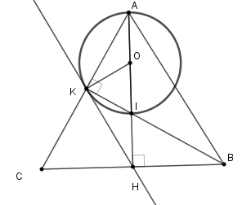
Gọi $O$ là trung điểm $AI$. Xét tam giác vuông $AIK$ có $OK = OI = OA \Rightarrow K \in \left( {O;\dfrac{{AI}}{2}} \right)$ (*)
Ta đi chứng minh $OK \bot KH$ tại $K$.
Xét tam giác $OKA$ cân tại $O$ ta có $\widehat {OKA} = \widehat {OAK}$ $\left( 1 \right)$
Vì tam giác $ABC$ cân tại $A$ có đường cao $AH$ nên $H$ là trung điểm của$BC$ . Xét tam giác vuông $BKC$ có $HK = HB = HC = \dfrac{{BC}}{2}$
Suy ra tam giác $KHB$ cân tại $H$ nên $\widehat {HKB} = \widehat {HBK}$$\left( 2 \right)$
Mà $\widehat {HBK} = \widehat {KAH}$ (cùng phụ với $\widehat {ACB}$) $\left( 3 \right)$
Từ $\left( 1 \right);\left( 2 \right);\left( 3 \right)$ suy ra $\widehat {HKB} = \widehat {AKO}$ mà $\widehat {AKO} + \widehat {OKI} = 90^\circ \Rightarrow \widehat {HKB} + \widehat {OKI} = 90^\circ \Rightarrow \widehat {OKH} = 90^\circ $ hay $OK \bot KH$ tại $K$ (**)
Từ (*) và (**) thì $HK$ là tiếp tuyến của đường tròn đường kính $AI$.
Hướng dẫn giải:
Sử dụng cách chứng minh tiếp tuyến
Để chứng minh đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm là $M$ ta chứng minh $OM \bot d$ tại $M$ và $M \in \left( O \right)$.

