Câu hỏi:
3 năm trước
Cho tam giác $A B O$ vuông tại \({\rm{O}}\), có góc \(BAO = {30^\circ },AB = a\). Quay tam giác $A B O$ quanh trục $A O$ ta được một hình nón có diện tích xung quanh bằng:
Trả lời bởi giáo viên
Đáp án đúng: d
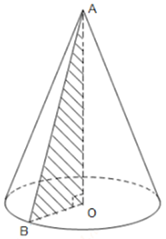
Công thức tính diện tích xung quanh hình nón: \({S_{xq}} = \pi R\ell \)
\(\begin{array}{l}R = OB,\ell = AB\\ \Rightarrow \sin {30^\circ } = \dfrac{{OB}}{{AB}}\\ \Rightarrow OB = AB \cdot \sin {30^\circ } = \dfrac{a}{2}\\ \Rightarrow {S_{xq}} = \pi R\ell = \pi \cdot \dfrac{{{a^2}}}{2}\end{array}\)
Hướng dẫn giải:
Công thức tính diện tích xung quanh hình nón: \({S_{xq}} = \pi R\ell \)


