Cho phương trình \({\left( {{x^2} - 2x + m} \right)^2} - 2{x^2} + 3x - m = 0\). Có bao nhiêu giá trị nguyên của \(m \in \left[ { - 10;10} \right]\) để phương trình đã cho có bốn nghiệm phân biệt

Chỉ điền các số nguyên, phân số dạng a/b

Đáp án:

Ta có:

\({\left( {{x^2} - 2x + m} \right)^2} - 2{x^2} + 3x - m = 0\)\( \Leftrightarrow {\left( {{x^2} - 2x + m} \right)^2} - 2\left( {{x^2} - 2x + m} \right) + m = x\)

Đặt \(a = {x^2} - 2x + m\), phương trình tên trở thành: \(x = {a^2} - 2a + m\)

Ta có hệ phương trình: \(\left\{ \begin{array}{l}a = {x^2} - 2x + m\\x = {a^2} - 2a + m\end{array} \right.\)

Trừ vế với vế hai phương trình trên ta được:

\(\begin{array}{l}a - x = \left( {{x^2} - 2x + m} \right) - \left( {{a^2} - 2a + m} \right)\\ \Leftrightarrow a - x = \left( {{x^2} - {a^2}} \right) - 2\left( {x - a} \right)\\ \Leftrightarrow \left( {x - a} \right)\left( {x + a} \right) - \left( {x - a} \right) = 0\\ \Leftrightarrow \left( {x - a} \right)\left( {x + a - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - a = 0\\x + a - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = a\\x + a - 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = {x^2} - 2x + m\\x + {x^2} - 2x + m - 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m =  - {x^2} + 3x\\m =  - {x^2} + x + 1\end{array} \right.\end{array}\)

 Vẽ trên cùng một đồ thị các Parabol: \(\left( {{P_1}} \right):y =  - {x^2} + 3x\), \(\left( P \right):y =  - {x^2} + x + 1\)

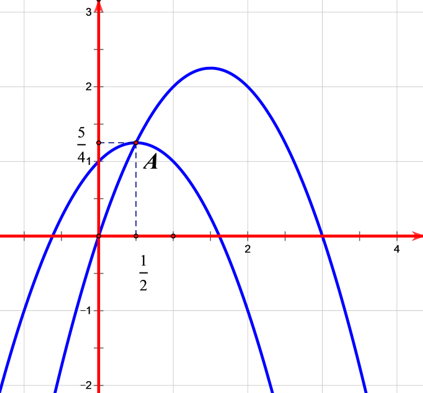
Quan sát đồ thị ta thấy để phương trình ban đầu có 4 nghiệm phân biệt thì đường thẳng \(y = m\) phải cắt cả 2 đồ thị trên tại 2 điểm phân biệt, tức là  \(m < \dfrac{5}{4}\)

Mà \( - 10 \le m \le 10\)

Nên \( - 10 \le m \le 1\)

Vậy có 12 giá trị của m thỏa mãn đề bài.