Câu hỏi:
3 năm trước
Cho phép tính \(\overline {ab} .\overline {cd} = 532.\) Biết \(\overline {ab} < \overline {cd} \), khi đó \(c\) bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: d
Vì \(\overline {ab} .\overline {cd} = 532\) nên \(\overline {ab} ,\overline {cd} \) là ước có hai chữ số của \(532.\)
Phân tích số \(532\) ra thừa số nguyên tố ta được:
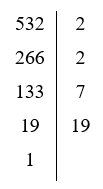
Hay \(532 = {2^2}.7.19 = 28.19 = 38.14\)
Suy ra \(\overline {ab} = 19\) thì \(\overline {cd} = 28\)
\(\overline {ab} = 14\) thì \(\overline {cd} = 38\)
Vậy \(c = 2\) hoặc \(c = 3.\)
Hướng dẫn giải:
Phân tích số \(532\) ra thừa số nguyên tố.
Từ đó tìm được \(\overline {ab} ;\overline {cd} \).

