Câu hỏi:
3 năm trước
Cho \(\left( {O;R} \right)\) và dây cung \(MN = R\sqrt 3 .\) Kẻ \(OI\) vuông góc với \(MN\) tại $I$ .
Tính số đo cung nhỏ $MN.$
Trả lời bởi giáo viên
Đáp án đúng: a
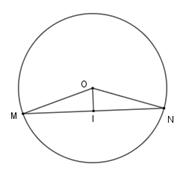
Xét tam giác $OIM$ vuông tại $I$ ta có $\sin \widehat {MOI} = \dfrac{{MI}}{{MO}} = \dfrac{{\sqrt 3 R}}{2}:R = \dfrac{{\sqrt 3 }}{2} \Rightarrow \widehat {MOI} = 60^\circ $
$\Delta MON$ cân tại $O$ có $OI$ vừa là đường cao vừa là đường phân giác nên $\widehat {MON} = 2\widehat {MOI} = 2.60^\circ = 120^\circ $
Suy ra số đo cung nhỏ $MN$ là $120^\circ $.
Hướng dẫn giải:
Sử dụng tỉ số lượng giác của góc nhọn và số đo cung
“Số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó”

