Câu hỏi:
3 năm trước
Cho nửa đường tròn $\left( O \right)$ đường kính $AB$. Trên tia đối của tia $AB$ lấy một điểm $M$. Vẽ tiếp tuyến $MC$ với nửa đường tròn. Gọi $H$ là hình chiếu của $C$ lên $AB$. Biết $MC = a,MB = 3a$. Độ dài đường kính $AB$ là?
Trả lời bởi giáo viên
Đáp án đúng: c
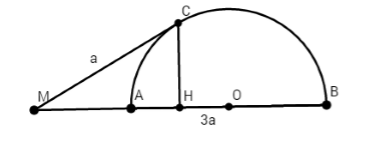
Ta có \(\widehat {MCA} = \widehat {CBA}\) (cùng chắn cung \(AC\))
Xét \(\Delta ACM\) và \(\Delta CBM\) có:
\(\widehat {MCA} = \widehat {CBA}\) (cmt)
\(\widehat M\) chung
Suy ra \(\Delta ACM \backsim \Delta CBM\) (g.g)
$\begin{array}{l} \Rightarrow M{C^2} = MA.MB\\ \Rightarrow MA = \dfrac{{{a^2}}}{{3a}} = \dfrac{a}{3}\\ \Rightarrow AB = MB - MA = 3a - \dfrac{a}{3} = \dfrac{{8a}}{3}\end{array}$
Hướng dẫn giải:
Chứng minh đẳng thức \(M{C^2} = MA.MB \Rightarrow MA \Rightarrow AB\).

