Câu hỏi:
2 năm trước
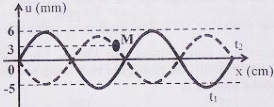
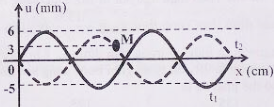
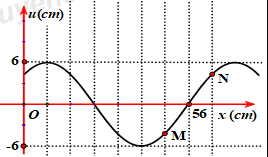
Cho một sợi dây cao su căng ngang. Làm cho đầu O của dây dao động theo phương thẳng đứng. Hình vẽ mô tả hình dạng sợi dây tại thời điểm \(t_1\) (đường nét liền) và \(t_2 =t_1+ 0,2s\) (đường nét đứt). Tại thời điểm \(t_3=t_2+ 0,4s\) thì độ lớn li độ của phần tử M cách đầu dây một đoạn \(2,4m\) (tính theo phương truyền sóng) là \(\sqrt 3 cm\). Gọi δ là tỉ số giữa tốc độ dao động cực đại của phần tử trên dây và tốc độ truyền sóng. Giá trị của δ là:
Trả lời bởi giáo viên
Đáp án đúng: b
- Từ đồ thị ta có: \(\lambda = 6,4m\)
Vận tốc truyền sóng: \(v = \dfrac{{\Delta {x_{12}}}}{{\Delta {t_{12}}}} = \dfrac{{7,2 - 6,4}}{{0,2}} = 4m/s\)
Tần số góc dao động của các phần tử: \(\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{\dfrac{\lambda }{v}}} = \dfrac{{2\pi v}}{\lambda } = \dfrac{{2\pi .4}}{{6,4}} = \dfrac{{5\pi }}{4}(ra{\rm{d}}/s)\)
- Độ lệch pha giữa M và O:
\(\Delta \varphi = \Delta {\varphi _x} + \Delta {\varphi _t} = \dfrac{{2\pi \Delta {x_{13}}}}{\lambda } + \omega \Delta {t_{13}} = \dfrac{{2\pi .2,4}}{{6,4}} + \dfrac{{5\pi }}{4}(0,2 + 0,4) = \dfrac{{3\pi }}{2}ra{\rm{d}}\)
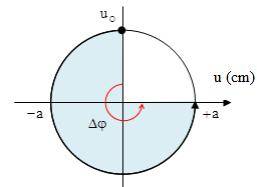
Từ vòng tròn lượng giác, ta có: \({u_M} = a = \sqrt 3 cm \to \delta = \dfrac{{\omega A}}{v} = \dfrac{{\dfrac{{5\pi }}{4}\sqrt 3 {{.10}^{ - 2}}}}{4} = 0,017\)
Hướng dẫn giải:
+ Đọc đồ thị và áp dụng các công thức sóng cơ học.
+ Sử dụng vòng tròn lượng giác
+ Áp dụng công thức tính độ lệch pha theo không gian và thời gian:
\(\Delta \varphi = \Delta {\varphi _t} + \Delta {\varphi _x} = \omega \Delta t + \dfrac{{2\pi \Delta x}}{\lambda }\)
Câu hỏi khác
- Bài tập các đại lượng đặc trưng của sóng cơ học có đáp án MÔN LÝ lớp 12
- Bài tập lí thuyết về sóng cơ và sự truyền sóng cơ có đáp án MÔN LÝ lớp 12
- Bài tập lý thuyết chung về giao thoa sóng có lời giải MÔN LÝ lớp 12
- Bài tập đồ thị sóng cơ học có đáp án MÔN LÝ lớp 12
- Bài tập phương trình sóng cơ học có đáp án MÔN LÝ lớp 12
