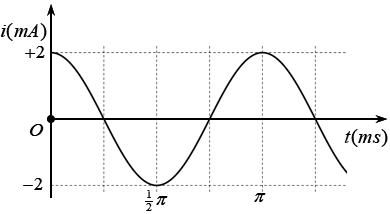
Cho một mạch dao động lí tưởng đang có dao động điện từ tự do. Hình bên là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện trong mạch i vào thời gian t. Tại thời điểm cường độ dòng điện trong mạch là 1mA thì điện tích trên tụ có độ lớn bằng
Trả lời bởi giáo viên
Từ đồ thị, ta có:
Chu kì dao động: \(T = \pi \left( {ms} \right) \Rightarrow \omega = \dfrac{{2\pi }}{T} = 2000\,\,rad/s\)
Cường độ dòng điện cực đại: \({I_0} = 2mA\)
Lại có: \({I_0} = \omega {q_0} \Rightarrow {q_0} = \dfrac{{{I_0}}}{\omega } = \dfrac{{{{2.10}^{ - 3}}}}{{2000}} = {10^{ - 6}}C\)
Ta có: \({\left( {\dfrac{q}{{{q_0}}}} \right)^2} + {\left( {\dfrac{i}{{{I_0}}}} \right)^2} = 1\)
\( \Leftrightarrow \dfrac{{{q^2}}}{{{{\left( {{{10}^{ - 6}}} \right)}^2}}} + {\left( {\dfrac{{{{10}^{ - 3}}}}{{{{2.10}^{ - 3}}}}} \right)^2} = 1 \Rightarrow \left| q \right| = 8,{66.10^{ - 7}}C\)
Hướng dẫn giải:
Sử dụng kĩ năng đọc và khai thác thông tin từ đồ thị.
Công thức liên hệ giữa cường độ dòng điện cực đại và điện tích cực đại: \({I_0} = \omega .{Q_0}\)
Sử dụng hệ thức độc lập theo thời gian: \({\left( {\dfrac{q}{{{q_0}}}} \right)^2} + {\left( {\dfrac{i}{{{I_0}}}} \right)^2} = 1\)
Câu hỏi khác
- Đề thi ĐGNL Hà Nội - Đề số 1 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 2 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 10 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 7 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
- Đề thi ĐGNL Hà Nội - Đề số 9 gồm 3 phần tư duy định tính, tư duy định lượng, khoa học xã hội 150 câu 195 phút có đáp án
