Cho lăng trụ đứng \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) có đáy là tam giác đều cạnh \(a\). Mặt phẳng \(\left( {A{B^\prime }{C^\prime }} \right)\) tạo với mặt đáy góc \({60^\circ }\). Tính theo \(a\) thể tích khối lăng trụ \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\).
Trả lời bởi giáo viên
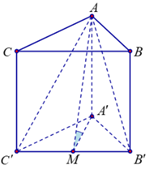
Gọi \(M\) là trung điểm \({B^\prime }{C^\prime }\)
Ta có \(\left\{ {\begin{array}{*{20}{l}}{{A^\prime }M \bot {B^\prime }{C^\prime }}\\{A{A^\prime } \bot {B^\prime }{C^\prime }}\end{array} \Rightarrow {B^\prime }{C^\prime } \bot AM} \right.\)
Nên góc giữa mặt phẳng \(\left( {A{B^\prime }{C^\prime }} \right)\) tạo với đáy là góc \(\widehat {AM{A^\prime }} = {60^\circ }\).
Tam giác \(A{A^\prime }M\) vuông tại \({A^\prime }\) nên \(A{A^\prime } = {A^\prime }M.\tan {60^\circ } = \dfrac{{3a}}{2}\)
Vậy thể tích khối lăng trụ \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) là \(V = A{A^\prime } \cdot {S_{{A^\prime }{B^\prime }{C^\prime }}} = \dfrac{{3{a^3}\sqrt 3 }}{8}\).
Hướng dẫn giải:
Chỉ ra góc giữa mặt phẳng \(\left( {A{B^\prime }{C^\prime }} \right)\) tạo với đáy là góc \(\widehat {AM{A^\prime }} = {60^\circ }\).


