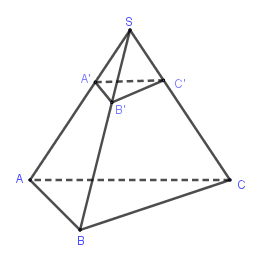
Cho khối chóp \(S.ABC\). Trên các cạnh \(SA,SB,SC\) lấy các điểm \(A',B',C'\) sao cho \(A'A = 2SA',B'B = 2SB',C'C = 2SC'\), khi đó tồn tại một phép vị tự biến khối chóp \(S.ABC\) thành khối chóp \(S.A'B'C'\) với tỉ số đồng dạng là:

\(\dfrac{1}{3}abc\)                

\(\dfrac{1}{9}abc\)

\(\dfrac{1}{6}abc\)    

\(\dfrac{2}{3}abc\)

Hình a

Hình c

Hình d

Hình b

\(D - C + M = 2\)        

$D + C - M = 2$

$D + C + M = 2$ 

$D - C + M = 0$

Hình tạo bởi hai tứ diện đều ghép với nhau là một đa diện lồi.

Tứ diện đều là đa diện lồi.

Hình lập phương là đa diện lồi 

Hình bát diện đều là đa diện lồi.

Hình 1

Hình 2

Hình 3

Hình 4

Mỗi cạnh của khối đa diện là cạnh chung của đúng $2$ mặt của khối đa diện.

Hai mặt bất kì của khối đa diện luôn có ít nhất một điểm chung.

Mỗi đỉnh của khối đa diện là đỉnh chung của ít nhất $3$  mặt.

Mỗi mặt của khối đa diện có ít nhất ba cạnh.