Cho khối chóp S.ABC có \(\left( {SAB} \right) \bot \left( {ABC} \right),\left( {SAC} \right) \bot \left( {ABC} \right)\), \(SA = a,AB = AC = 2a,BC = 2a\sqrt 2 \). Bình phương của cosin góc giữa (SAC) và (SBC) bằng
Chỉ được phép điền số 0, nguyên âm, nguyên dương và phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
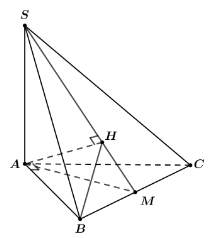
Gọi M là trung điểm của BC\( \Rightarrow AM \bot BC\)
Kẻ \(AH \bot SM\) tại H
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAC} \right) \bot \left( {ABC} \right)\end{array} \right. \Rightarrow SA \bot \left( {ABC} \right)\)
\(\left. \begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\AB = AC\end{array} \right\} \Rightarrow \Delta ABC\) vuông tại A.
Ta có: \(BC \bot SA \Rightarrow BC \bot \left( {SAM} \right)\)\( \Rightarrow BC \bot AH\)
\( \Rightarrow AH \bot \left( {SBC} \right)\)
Ta lại có: \(AB \bot \left( {SAC} \right)\)
=> Góc giữa (SAC) và (SBC) bằng góc giữa AH và AB và bằng \(\widehat {HAB}\)
Ta có: \(AM = \dfrac{{BC}}{2} = a\sqrt 2 \)\( \Rightarrow AH = \dfrac{{AM.SA}}{{\sqrt {A{M^2} + S{A^2}} }} = \dfrac{{a\sqrt 6 }}{3}\)
\( \Rightarrow \cos \widehat {HAB} = \dfrac{{AH}}{{AB}} = \dfrac{{\dfrac{{a\sqrt 6 }}{3}}}{{2a}} = \dfrac{{\sqrt 6 }}{6}\)
Vậy bình phương của cosin góc giữa (SAC) và (SBC) bằng \(\dfrac{1}{6}\)
Hướng dẫn giải:
Gọi M là trung điểm của BC\( \Rightarrow AM \bot BC\)
Kẻ \(AH \bot SM\) tại H


