Cho hypebol $(H):\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\,\,(b > a > 0)$. Cho $k$ là một số thực dương. Xét các đường thẳng $({d_1}):\,\,y = kx,$$({d_2}):\,\,y =  - \dfrac{1}{k}x$ đều cắt $(H)$ tại $2$ điểm phân biệt. Gọi $A$ và $C$ lần lượt là giao điểm của $({d_1})$ với $(H)$ ($A$ nằm trong góc phần tư thứ nhất). Gọi $B$ và $D$ lần lượt là giao điểm của $({d_2})$ với $(H)$ ($B$ nằm trong góc phần tư thứ hai). Tìm $k$ sao cho hình thoi $ABCD$ có diện tích nhỏ nhất.

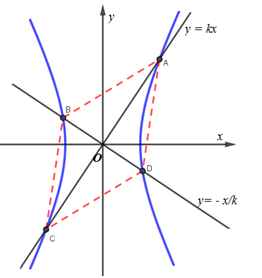
Giả sử phương trình đường thẳng $AC$ là $y = kx$

Tọa độ của $A$ là nghiệm của hệ phương trình $\left\{ \begin{array}{l}y = kx\\\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = kx\\\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{k^2}{x^2}}}{{{b^2}}} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y^2} = {k^2}{x^2}\\{x^2}\left( {\dfrac{1}{{{a^2}}} - \dfrac{{{k^2}}}{{{b^2}}}} \right) = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} = \dfrac{{{a^2}{b^2}}}{{{b^2} - {k^2}{a^2}}}\\{y^2} = \dfrac{{{k^2}{a^2}{b^2}}}{{{b^2} - {k^2}{a^2}}}\end{array} \right.$

$\Rightarrow O{A^2} = {x^2} + {y^2} = \dfrac{{{a^2}{b^2}}}{{{b^2} - {k^2}{a^2}}} + \dfrac{{{k^2}{a^2}{b^2}}}{{{b^2} - {k^2}{a^2}}} = \dfrac{{\left( {1 + {k^2}} \right){a^2}{b^2}}}{{{b^2} - {k^2}{a^2}}} \Rightarrow \dfrac{1}{{O{A^2}}} = \dfrac{{{b^2} - {k^2}{a^2}}}{{\left( {1 + {k^2}} \right){a^2}{b^2}}}$

Chứng minh tương tự ta được $O{B^2} = \dfrac{{\left( {1 + {k^2}} \right){a^2}{b^2}}}{{{k^2}{b^2} - {a^2}}} \Rightarrow \dfrac{1}{{O{B^2}}} = \dfrac{{{k^2}{b^2} - {a^2}}}{{\left( {1 + {k^2}} \right){a^2}{b^2}}}$

$\begin{array}{l} \Rightarrow \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{{{b^2} - {k^2}{a^2}}}{{\left( {1 + {k^2}} \right){a^2}{b^2}}} + \dfrac{{{k^2}{b^2} - {a^2}}}{{\left( {1 + {k^2}} \right){a^2}{b^2}}}\\ = \dfrac{{{b^2}\left( {1 + {k^2}} \right) - {a^2}\left( {1 + {k^2}} \right)}}{{\left( {1 + {k^2}} \right){a^2}{b^2}}} = \dfrac{{{b^2} - {a^2}}}{{{a^2}{b^2}}} = \dfrac{1}{{{a^2}}} - \dfrac{1}{{{b^2}}} = const\end{array}$ 

Khi đó:

$\begin{array}{l}\dfrac{1}{{{a^2}}} - \dfrac{1}{{{b^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}}\mathop  \ge \limits^{Cauchy} \dfrac{2}{{OA.OB}} = \dfrac{4}{{{S_{ABCD}}}}\\ \Leftrightarrow \dfrac{{{b^2} - {a^2}}}{{{a^2}{b^2}}} \ge \dfrac{4}{{{S_{ABCD}}}} \Leftrightarrow {S_{ABCD}} \ge \dfrac{{4{a^2}{b^2}}}{{{b^2} - {a^2}}}\\ \Rightarrow {S_{ABCD\,Min}} = \dfrac{{4{a^2}{b^2}}}{{{b^2} - {a^2}}} \Leftrightarrow OA = OB\end{array}$

$\Leftrightarrow \Delta OAB$ vuông cân tại $O$

$\Rightarrow y = kx$ là tia phân giác của góc phần tư thứ $I$

$\Rightarrow k = 1$