Câu hỏi:
2 năm trước
Cho hình vuông $ABCD,{\rm{ }}E$ là một điểm trên cạnh $CD.$ Tia phân giác của góc $BAE$ cắt $BC$ tại $M.$ Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: c
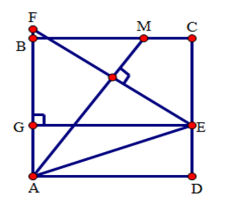
Vẽ $EF \bot AM(F \in AB),EG \bot AB(G \in AB)$.
Tứ giác $AGED$ là hình chữ nhật( vì \(\widehat G = \widehat A = \widehat D = {90^0}\) ), suy ra $GE = AD.$
Lại thấy \(\widehat {FEG} = \widehat {MAB}\) (vì cùng phụ với \(\widehat {AFE}\) )
Xét \(\Delta GEF\) và \(\Delta BAM\)có: \(\widehat {EGF} = \widehat {ABM} = {90^0}\); $GE = AB{\rm{ }}\left( { = CD} \right);$\(\widehat {FEG} = \widehat {MAB}\)
Do đó \(\Delta GEF = \Delta BAM\)(g.c.g) suy ra $EF = AM.$
Tam giác $AEF$ có $AM$ là đường phân giác và là đường cao nên tam giác $AEF$ cân đỉnh $A.$
Ta có $AM$ là đường trung trực của $EF,$ nên $ME = MF.$
Xét ba điểm $M,{\rm{ }}E,{\rm{ }}F$ ta có: \(EF \le ME + MF \Leftrightarrow EF \le 2ME\). Do đó \(AM \le 2ME\).
Hướng dẫn giải:
Vẽ $EF \bot AM(F \in AB)$
Chứng minh $EF = AM.$
Chứng minh tam giác $AEF$ cân đỉnh$A.$
Chỉ ra $ME = MF.$
Xét ba điểm $M,{\rm{ }}E,{\rm{ }}F$ ta có: \(EF \le ME + MF\) để suy ra hệ thức đúng.
