Trả lời bởi giáo viên
Đáp án đúng: d
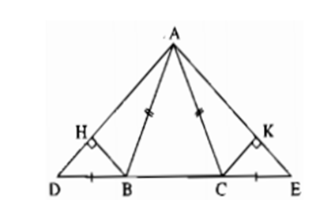
Vì tam giác \(ABC\) cân tại \(A\) (do \(AB = AC\) ) nên \(\widehat {ABC} = \widehat {ACB}\) (tính chất) (1)
Lại có \(\widehat {ABC} + \widehat {ABD} = 180^\circ \) và \(\widehat {ACB} + \widehat {ACE} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {ABD} = 180^\circ - \widehat {ABC}\) ; \(\widehat {ACE} = 180^\circ - \widehat {ACB}\) (2)
Từ (1) và (2) suy ra \(\widehat {ABD} = \widehat {ACE}\)
Xét tam giác \(ABD\) và tam giác \(ACE\) có
\(AB = AC;\,\)\(\widehat {ABD} = \widehat {ACE}\,\left( {cmt} \right);\)\(BD = CE\,\)
Suy ra \(\Delta ABD = \Delta ACE\left( {c - g - c} \right)\) \( \Rightarrow \widehat {DAB} = \widehat {CAE}\) (hai góc tương ứng)
Xét tam giác \(AHB\) và \(AKC\) có
+ \(\widehat H = \widehat K = 90^\circ \)
+ \(AB = AC\)
+ \(\widehat {DAB} = \widehat {CAE}\,\left( {cmt} \right)\)
Suy ra \(\Delta AHB = \Delta AKC\,\left( {ch - gn} \right)\)
Hướng dẫn giải:
+ Chứng minh hai tam giác \(BAD\) và \(CAE\) bằng nhau theo trường hợp cạnh- cạnh- cạnh để suy ra \(\widehat {DAB} = \widehat {CAE}\)
+ Từ đó chứng minh hai tam giác vuông \(AHB\) và \(AKC\) bằng nhau theo trường hợp cạnh huyền-góc nhọn.
Câu hỏi khác
- Bài tập trắc nghiệm Tổng các góc trong một tam giác môn Toán lớp 7 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Trường hợp bằng nhau thứ hai và thứ ba của tam giác môn Toán lớp 7 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Các trường hợp bằng nhau của tam giác vuông môn Toán lớp 7 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác môn Toán lớp 7 sách KNTTVCS có lời giải
- Bài tập trắc nghiệm Tam giác cân. Đường trung trực của đoạn thẳng môn Toán lớp 7 sách KNTTVCS có lời giải
