Câu hỏi:
2 năm trước
Cho hình vẽ như sau:
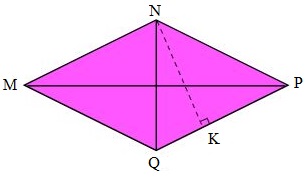
Hình thoi MNPQ có độ dài cạnh là \(32cm\). Tổng độ dài hai đường chéo là \(84cm\), hiệu độ dài hai đường chéo là \(12cm\). Độ dài chiều cao NK là:
Trả lời bởi giáo viên
Đáp án đúng:
A. \(27cm\)
Ta có sơ đồ:
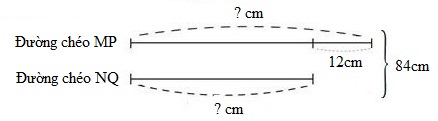
Độ dài đường chéo MP là:
\((84 + 12):2 = 48\left( {cm} \right)\)
Độ dài đường chéo NQ là:
\(84 - 48 = 36\,\,\left( {cm} \right)\)
Diện tích hình thoi đó là:
\(48 \times 36:2 = 864\left( {{m^2}} \right)\)
Độ dài chiều cao NK là:
\(864:32 = 27\,\,(cm)\)
Đáp số: \(27cm\).
Hướng dẫn giải:
- Ta có tổng và hiệu của hai đường chéo. Ta sẽ tìm hai đường chéo theo công thức tìm hai số khi biết tổng và hiệu của hai số đó:
Số lớn = (Tổng + Hiệu) \(:\,\,2\) ; Số bé = (Tổng – hiệu) \(:\,\,2\)
- Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho \(2\) .
- Vì hình thoi có các cặp cạnh đối diện song song và bằng nhau nên hình thoi cũng chính là hình bình hành. Để tính độ dài chiều cao NK ta lấy diện tích chia cho độ dài cạnh đáy PQ.
.jpg)
