Câu hỏi:
2 năm trước
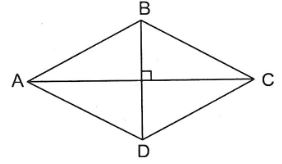
Cho hình vẽ như sau:
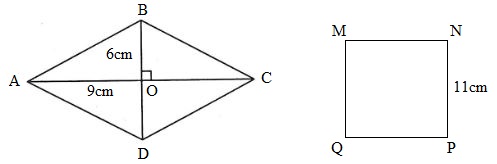
Hình thoi ABCD có O là giao điểm của hai đường chéo, \(OA = 9cm,\,\,OB = 6cm\). Biết rằng hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường. Em hãy chọn khẳng định đúng:
Trả lời bởi giáo viên
Đáp án đúng:
C. Diện tích hình thoi bé hơn diện tích hình vuông.
Độ dài đường chéo AC là:
\(9 \times 2 = 18\,\,(cm)\)
Độ dài đường chéo BD là:
\(6 \times 2 = 12\,\,(cm)\)
Diện tích hình thoi ABCD là:
\(18 \times 12:2 = 108\,(c{m^2})\)
Diện tích hình vuông MNPQ là:
\(11 \times 11 = 121\,(c{m^2})\)
Mà: \(108c{m^2} < 121c{m^2}\)
Vậy diện tích hình thoi bé hơn diện tích hình vuông.
Hướng dẫn giải:
- Tính độ dài đường chéo AC, BD: \(AC = OA \times 2\,\,;\,\,\,BD = OB \times 2\,\).
- Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho \(2\).
- Tính diện tích hình vuông ta lấy cạnh nhân với cạnh.
- So sánh hai số đo diện tích rồi rút ra kết luận.
.jpg)
