Câu hỏi:
2 năm trước
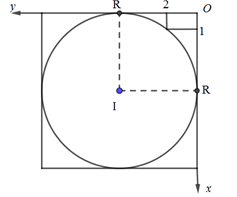
Cho hình trụ $(T)$ có $\left( C \right),\,\,\left( {C'} \right)$ là hai đường tròn đáy nội tiếp hai mặt đối diện của một hình lập phương. Biết rằng, trong tam giác cong tạo bởi đường tròn $(C)$ và hình vuông ngoại tiếp của $(C)$ có một hình chữ nhật kích thước $1 \times 2$ (như hình vẽ dưới đây). Thể tích của khối trụ $(T)$ là
Trả lời bởi giáo viên
Đáp án đúng: a
Gắn hệ trục tọa độ trong mặt phẳng chứa đường tròn $(C)$ như hình vẽ.
Phương trình đường tròn $(C):$ ${\left( {x - R} \right)^2} + {\left( {y - R} \right)^2} = {R^2},\,\,\,(R > 2)$
Điểm $\left( {1;2} \right)$ thuộc (C)$ \Rightarrow {\left( {1 - R} \right)^2} + {\left( {2 - R} \right)^2} = {R^2} \Leftrightarrow {R^2} - 6R + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}R = 1\,\,(L)\\R = 5\end{array} \right. \Leftrightarrow R = 5$
$ \Rightarrow $ Chiều cao của khối trụ $h = 2R = 10$
Thể tích khối trụ là: $V = \pi {R^2}h = \pi {.5^2}.10 = 250\pi $.
Hướng dẫn giải:
- Gắn hệ trục tọa độ trong mặt phẳng chứa đường tròn $(C)$, tìm bán kính của đường tròn $\left( C \right)$.
- Tính thể tích khối trụ.
Câu hỏi khác
- Đề thi kiểm tra 1 tiết chương 6: Mặt nón, mặt trụ, mặt cầu - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 3 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 1 tiết chương 6: Mặt nón, mặt trụ, mặt cầu - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra 15 phút chương 6: Mặt nón, trụ, cầu - Đề số 2 Toán 12 có lời giải chi tiết
